Introduction
Railroad lines are often high demanded and - caused by high building costs and times - in middle-term not expandable. So in an economical point of view railroad infrastructure can be qualified as a "scarce good". Using this good as efficient as possible is one of the basic goals in commerce and so it is in railway scheduling.
The question to find a valid usage of tracks and stations (i.e. a set of conflict free train routes) with respect to given train requests is called "Train Timetabling Problem" (abbr. TTP). Also common synonyms used in literature are "Train Scheduling Problem", "Track Allocation Problem" and "Train Routing Problem".
In our setting the degrees of freedom are on the one hand the decision which trains to schedule or to reject and on the other the detailed macroscopic route in space and time of each choosen train request. It is clear that there is no "the" train timetabling problem. Nevertheless we try to formulate a general specification of the problem - which gives anybody the possibility to reformulate most of the common variations of the problem. We invite users to participate in development and bring their needs and experience into future versions of our XML schemes. Furthermore we want explicit point out that we are focused on macroscopic railway data. For microscopic data handling we refer to the railML standard.
Computing an efficient or (better optimal) train timetable is a hard combinatorial problem in organizing railway traffic. Apart from the lack of available railway data and economic quantification of timetables, even the pure mathematical or computational problem is a great challenge. Caprara, Fischetti and Toth showed 2002 that this problem is NP-hard. A proof by reduction to the famous Maximum Independent Set Problem was given. This somehow expresses that from a complexity point of view the Train Timetabling Problem belongs to the "toughest" problems, such as the Traveling Salesman Problem, in theoretical computer science. This motivates the introduction of this library; provide data needed for comparisons on the competitiveness of different approaches.
Macroscopic Data
As mentioned above, we assume a railway infrastructure on a macroscopic level. A network consists of stations and tracks. A track is directed and can only be used by one train at each time. By definition overtaking is not possible on a single track and only allowed inside stations; but it is possible to declare additional pseudo points (for line crossings or sidings) in the network, so called pseudo-stations to deal with overtaking on the railroad. Besides this special type of stations, we handle dead-end (only one side) and standard stations (exactly two sides 1 and 2 to enter and leave). In addition to the start and end station for each track; we also need the information which side of the stations are connected by this track. This is needed for a feasible consideration of turnaround times.
Trains belong to a specified aggregated traintype. A tree structure helps to build up the hierarchy of these sets, i.e. look at entity traintypetree here. For each traintype all properties of the higher level train type are valid; analogously restrictions of the higher level train type has to be fulfilled, as well as the traintype specific ones.
Routing trains
All times are discretized to some defined unit (in number of seconds, default macroscopic discretization would be 60). A train route on a macroscopic view is a path in time and space through a suitable digraph. The nodes of the digraph correspond to events at the stations in time. To reflect realistic behaviour of trains, we consider three possible events inside a normal station - arrival, departure (not allowed for pseudo stations) and passing (for each side). Resulting in node types:
- arrival,
- departure,
- passing.
This gives an intuition of the nodes (tupels of station, side, node-type and train-type) of the train scheduling digraph. These nodes are now suitable connected by directed arcs - representing certain activities. At the moment three different kinds are covered by our model, driving (on tracks), changing the direction of the train (turnaround) and waiting inside a station. A turnaround inside a station specifies the minimal time a train of this type needs to enter and leave this station in on the same side. The interface uses the term turnaround_times.
Due to the fact that running times or drive times highly depend on the status (velocity, weight...) of the train at the beginning and at the end of the considered track, we distinguish between four different main drive modes:
- 1. combination stop at start - stop at end,
- 2. combination stop at start - pass at end,
- 3. combination pass at start - stop at end,
- 4. combination pass at start - pass at end.
Track safety
Instead of block section exclusivitiy, which is handled on a highly detailed microscopic stage - we only ensure track safety w.r.t. given minimal headway times at departure. For each driving arc we need the information what is the next possible time a train (depending on the train type) can enter this track - driving in the same direction.
- arcs on tracks of opposite directions (so called single tracks),
- arcs on tracks of same-level-crossings, sidings, intersections,
- restrictions on meeting points (tunnels, oversized equipment)
- etc.
Station capacity
At any point in time, certain station capacities has to be fulfilled. These define the maximal number of trains of a given traintype that can be handled; we distinguish between:
- platform capacity,
- running capacity,
- overall capacity.

Request set
Second input of an instance of the train timetabling problem is a set of requested trains. Naturally, these are coming from train operators and not from infrastructure managers as the infrastructure input. That is one reason why we decided to split the input in these both parts. Nevertheless, each instance of the train timetabling problem consist of exactly one infrastructure and one request set. Obviously there must be a suitable correspondence between them.
Slot requests
First of all we describe mandatory information to each single train or slot request. A valid train type for a feasible routing and a positive basis profit value for a meaningful optimization is needed. Furthermore exactly one departure station and one arrival station has to be declared, see StartSlotRequestStop and FinalSlotRequestStop. Their preferences for arrival and departure are defined by some window time, consisting of ascending minimal, optimal and maximal time. Clearly all times are with respect to to the time unit of the network, i.e. in minutes. If a train is scheduled, but the optimal arrival and departure times are not met, his profit value decreases linear in time by some given penalty. For each case - early or late departure or arrival - is it possible to define a different penalty depending on the purpose of the request.
Additionally one can specify some optional requirements and informations, like train names or train operator. Predefined trains should be given as train request with a true flag fixed. Then this train has to be scheduled or no feasible solution of the train timetabling problem exists. Mainly for passenger traffic it is desired to specify intermediate stops. In this case we need information to arrival and departure. Optionally, the time this train should wait inside this station can be given by an intervall, see DwellingTime.
Solution
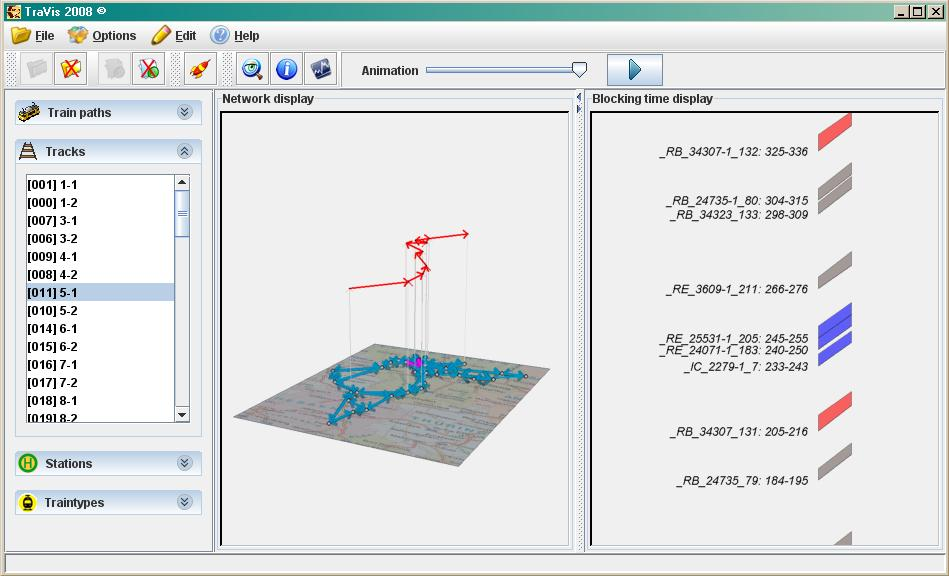
A solution of an instance of the train timetabling problem - a macroscopic feasible timetable - is specified by a list of the scheduled trains and their course through the network. Accordingly, for each train request, we expect a sorted list of stations with arrival and departure time and a list of connecting tracks. Furthermore objective values of each path and of the entire solution, user-specific station and track labels and valid upper bounds can be optionally specified. All these information to a solution together with the network can be visualized by TraVis.


