Example

On this page we give a small example of the train scheduling problem. We will see that even a small instance can lead to a great variety of possible solutions and is therefore nearly impossible to solve by hand. As you will see the greedy algorithm - i.e. choosing successively the most profitable request - will lead to solution far away from optimality.

Network instance

Let's assume that we have given the following network with a single line and six train stations.

Easiest imaginable network - a path.

Note: We can interprete this figure as a graph whereas the nodes represent the stations and the arcs represent the railtracks.

Problem Constraints

For simplicity we require that no headway constraints are given and that the given request only contains valid drivetimes. Also suppose that we have no station capacities to regard. So the only constraint we want to consider is that trains can't pass each other.

Request instance

Now suppose that the network operator has given 17 slot requests as outlined in the following figure. The numbers listed there represent the gain with an arbitrary monetary unit (MU) - e.g. € or $ - for the operator if he decides to accept that train request. The horizontal move of a request outlines the time needed for that trip and the vertical movement represents the position in that time.

With this notation an overhauling is represented by an intersection of to arcs. So the question to find a conflict-free (i.e. valid) timetable is here equivalent to find an intersection-free subset of arcs in this illustration.

Possible lines and their profits.

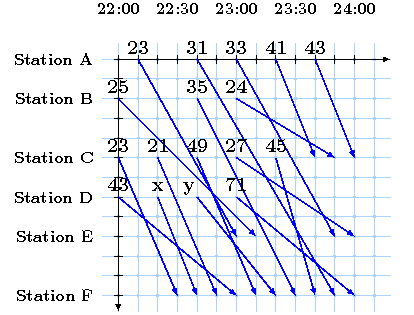
Since we don't want to bore you, we decided to leave the revenue for two of these slot-requests variable. But before reading on take time and try to solve this example to optimality.

Note: The figure can also be regarded as a time-expansion of the above network-graph.

Solutions

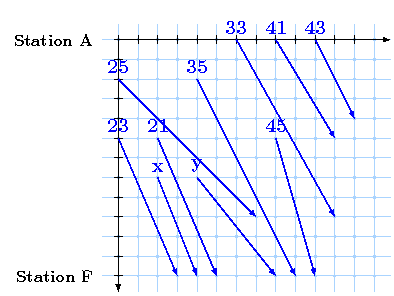
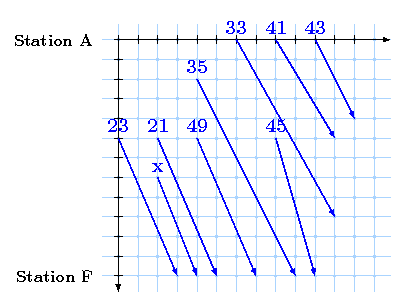
Solving the non-variable part can easily be done by trial and error or encounting all possibilities. Maybe you also noticed that the problem can be devided into three subproblems which can be solved independently. As you see the "x"-request increases the gain for the network operator while x > 0. So in this case we would choose this request and the "neighboured" requests with revenue 21 and 23 MU istead of the conflicting request with the revenue of 43 MU. We also notice that choosing the most profitable train won't lead to an optimal solution.

Now let's have a look at the "y"-train. We have the choice either to accept this train and a train with a value of 25 MU or to accept a train with value of 49 (or a train with value 23). So we have to decide wheter 25 + y ≥ 49 holds or not.

1. Solution if y ≥ 24 with value 266 + x + y

2. Solution if y < 24 with value 290 + x

Problems of this dimension can nowadays be solved with optimization tools by a fraction of a second. It's very likely that it would take longer to read-in the data-files containing the necessary informations then to solve it. If you review how long it took to solve the above problem by hand, you may imagine how long it would took to solve realistic instances by hand.